センサデータに「ゆっくりとした変動」や「ドリフト」が含まれていて、本当に注目したい瞬間的な変化が埋もれてしまう。
そんな経験はありませんか?
そんなときに活躍するのがHPF(ハイパスフィルタ)です。
HPF(ハイパスフィルタ)を使えば、信号の中から急激な変化や高周波成分だけを抽出することができるので、異常検知や動きの検出など、IoT分野でも非常に有効です。
この記事では、HPFの基本的な仕組みと考え方を始め、ローパスフィルタとの関係や実装方法などについて解説していきます。
HPF(ハイパスフィルタ)のフロー概要
HPF(ハイパスフィルタ)のテスト用フローの完成形を示します。
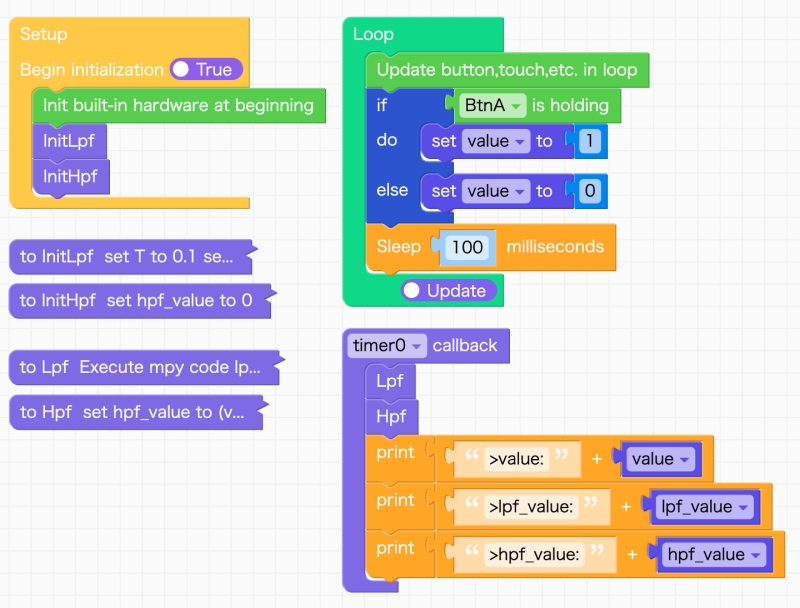
Setupブロック
- LPFのイニシャライズ
- HPFのイニシャライズ
Loopブロック
- フィルターへの入力信号の処理
タイマーコールバック関数
- ローパスフィルタの計算
- ハイパスフィルタの計算
- デバッグ用シリアル出力
HPF(ハイパスフィルタ)の実行結果
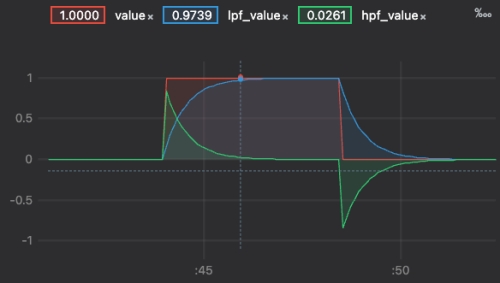
入力信号(赤色)に対して、ハイパスフィルタ(緑色)の信号を抽出できます。
入力信号の変化を捉えていることがわかります。
HPF(ハイパスフィルタ)の計算式
ハイパスフィルタは、ローパスフィルタの出力を利用して計算できます。
入力信号:value
ローパスフィルタの出力:LPF(value)
とすると
HPF(value) = value - LPF(value)
と表すことができます。
LPF(ローパスフィルタ)についてはこちらの記事を参考にしてください。
実装例
ローパスフィルタ
lpf_value = alpha × value + ( 1 - alpha ) × lpf_value_prev
- value : 入力信号
- lpf_value : ローパスフィルタ出力
- lpf_value_prev : 前回のローパスフィルタ出力
- alpha : ローパスフィルタ係数
- alpha = T / ( T + Ti ) T : サンプリング周期 Ti : 時定数
ハイパスフィルタ
hpf_value = value - lpf_value
- hpf_value : ハイパスフィルタ出力
HPF(ハイパスフィルタ)のフロー詳細

HPF(ハイパスフィルタ)の詳細について説明します。
Setupブロック
関数 InitLpf と 関数 InitHpf を実行して計算のイニシャライズを行います。
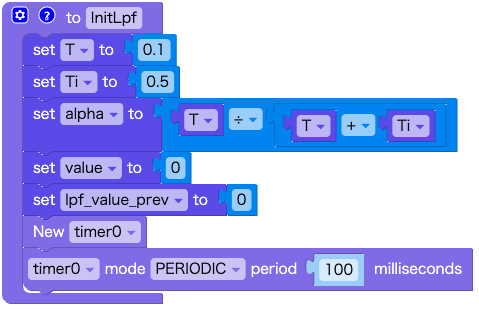
LPF(ローパスフィルタ)の計算に使用する変数の初期値を設定します。
- 変数 T[sec]:サンプリング周期
- 変数 Ti[sec]:時定数
- 変数 alpha: T / ( T + Ti )
- 変数 value:LPFに入力する値
- 変数 lpf_value_prev:前回のLPF出力値

hpf_value の初期値を設定
Loopブロック
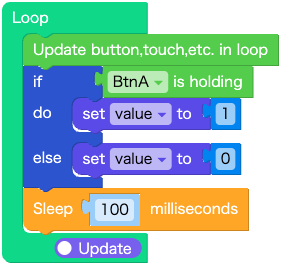
Loopブロックでは、ボタンのオンオフでフィルターの入力値を変化させます。
- ボタンを押している時は、1
- ボタンを離している時は、0
となるように値を設定します。
この処理を100msec周期で繰り返します。
タイマーコールバック関数
Setupブロックで設定しているように、このタイマーコールバック関数は100secごとに呼び出されます。
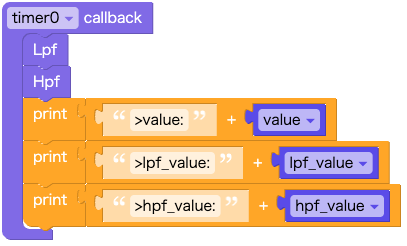
ローパスフィルタの計算(関数)、ハイパスフィルタの計算(関数)および、デバッグ用のシリアル出力からなります。
関数: LPF

ローパスフィルタの計算式は少し複雑なので、ここではPythonコード実行ブロックに数式を記述しています。
ローパスフィルタ計算の後に、計算結果 lpf_value を lpf_value_prevに保存します。
関数:Hpf
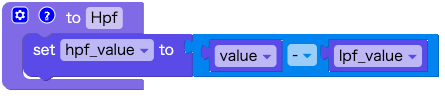
ハイパスフィルタの計算式を記述します。
実行結果

上図は、M5Stackのシリアル出力を使って、フィルタの計算結果をプロットしたものです。
入力信号(赤色)に対して、HPF(ハイパスフィルタ)の出力(緑色)の特徴は次の通り。
- 入力信号の変化を抽出している
- 変化がない時は、HPFの出力はゼロ
HPF(ハイパスフィルタ)が正しく動作していることを確認できました。
別の記事では、実際のアプリケーションでHPFを使った事例について紹介していきます。
